|
|
Four basic tile shapes I use are eqilateral triangle, square, rhombus, and regular pentagon. The square is just under
an inch and a half across.
|
|
|
All five of the Platonic solids can be made using tile shapes pictured above (except rhombus). Starting at the
lower right and going clockwise there are: tetrahedron, cube, octahedron, dodecahedron, and icosahedron. 4, 6, 8, 12,
and 20 sides respectively.
|
|
|
This polyhedron has 12 identical sides and is known as a rhombic dodecahedron. Some of the vertex points are formed
by 4 sides, and others are formed by 3 sides. Objects with this shape have the ability to be stacked without leaving
any open space between them. Cubes can also do this along with a few other combinations of shapes. This shape
is also formed in the interior of the shape shown in the next picture below.
|
|
|
I call this a "squareball". It is made entirely out of square tiles. 3 tiles are joined into a
triangular prism, then four of these prisms are joined together into a tetrahedron. There are 8 tetrahedrons used to
make a "squareball" as shown. 96 square tiles are needed to make a squareball, but if you eliminate the 8
triangular prisms protruding out then you would only need 72 tiles. Notice that there are some un-paired box joints
left open, these can be joined with other squareballs or other shapes to create a larger object.
|
|
|
A squareball split into halves. The entire structure fits together with friction-fit box joints, and the tiles can be
taken apart and put back together in many ways.
|
|
|
A quarter of a squareball. Two tetrahedrons connected at two edges. The squareballs can be put together and
taken apart rapidly by constructing tetrahedrons from triangular prisms rather than adding individual tiles or prisms individually
to the structure.
|
|
|
An object made up of hundreds of square tiles. As the structure grows you will be able to see the overlapping nature
as spherical shapes share tiles. There are several types of symmetry in this kind of structure including tetrahedral,
cubic, and octahedral. The square tiles can be used to model different crystalline structures, or lattices.
|
|
|
A large cube made up of squareball units. Luckily I am not OCD and this is as big as I let it get. :)
It is made of 8 squareballs for a total of 768 tiles.
|
|
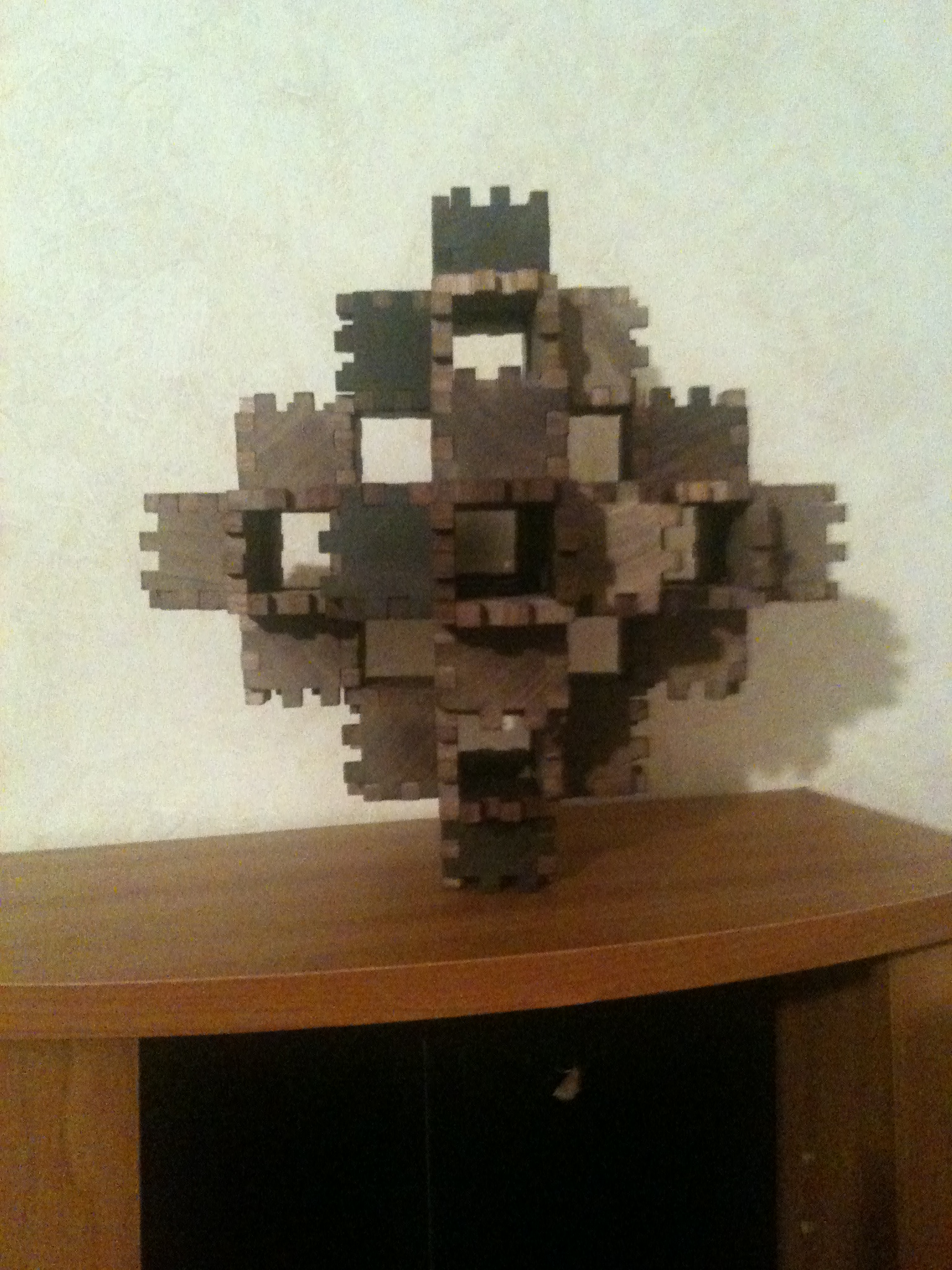
|
A more familiar kind of symmetry made with square tiles - cubic.
|
|

|
At first glance, this structure appears to be another example of the squareballs shown above - it is not. This
structure is an attempt at pentagonal symmetry - and it worked somewhat until I tried to make it larger. The problem
is that the angle between sides of a REGULAR pentagon is 108°, and the angle between corners of a tetrahedron passing
through the center is 109.5°. This small error can be taken up by the box joints as long as the structure is small.
The effect of the error is cumulative though and if you were to try to try to expand the structure further the joints will
pull apart. No stable crystalline structure contains regular pentagons.
|
|
|
The tiles can also be used to create flat designs. This pentagonal pattern has 5-fold symmetry. The dark
squares are walnut that has been finished with mineral oil. Dampen a sponge or cloth with mineral oil very sparingly.
Rub in only enough to darken the wood. Excess oil may cause box joints to swell enough to not fit.
|
|
|
Not all polyhedrons are spherical, this one is elliptical and looks like either an Easter egg, or a football. It
is made of 8 pentagons, 26 squares, and 16 triangles. Measures 6.5 inches long and 5 inches diameter.
|
|
|
12 Rhombus tiles and 30 squares.
|
|
|
This polyhedron uses the same tiles as a regular dodecahedron and a regular icosahedron. 12 pentagons and 20 triangles.
|
|
|
This is was the largest sphere I have made with the tiles, it is the
same shape as the one pictured above plus it also has a square inserted at each edge. 12 pentagons, 20 triangles, and
60 squares. Measures 7 3/4 inches in diameter.
|
|
|
I thought it would be neat to see how much larger I could make the ball in the picture above if I added 2 squares instead
of just one. This one measures 11 1/2 inches in diameter. 20 triangles, 12 pentagons, and 120 squares. I suppose
it could be made larger still, but it would also become more fragile. Would be fun to make special tiles to fill the
open spaces, glue it together and turn it smooth on a lathe.
|
| |
|
| |
|
| |
|

